• Physics 16, 151
A new set of equations captures the dynamic interactions of electrons and vibrations in crystals and forms the basis of computational studies.
J. Berges/University of Bremen
Although a crystal is a highly ordered structure, it is never at rest: its atoms are constantly vibrating about their equilibrium positions – up to zero temperature. Such vibrations are called phonons, and their interaction with the electrons that hold the crystal together is part of the properties of the crystal, its ability to conduct heat or electricity, and its resistance to electricity if it is superconducting. Predicting, or at least understanding, those structures requires an accurate description of the interaction of electrons and phonons. This task is daunting because the electronic problem alone—assuming atomic nuclei are stationary—is already challenging and has no exact solution. Now, based on a long list of previous key events, Gianluca Stefanucci of Rome’s Tor Vergata University and his colleagues have made an important step toward a complete theory of electrons and phonons. [1].
At a lower level of theory, the electron-phonon problem is simplified. First, one considers the arrangement of mass charges representing the electrons and nuclei of atoms. Second, one allows these charges to evolve under Coulomb’s law and the Schrödinger equation, which can introduce periodic disturbances. The mathematical representation of the dynamics of such a system, including kinetic and interaction terms, is the Hamiltonian of the system. However, knowing the actual theory is not enough because the corresponding equations are formally simple. In fact, they are so complex—not least because of the large number of particles involved—that guesswork is required. Therefore, at a high level, functional theory must provide methods for making reasonable approximations that produce equations that can be solved on modern computers.
One way to reduce the complexity of the problem is to fall back on the individual particle picture in favor of one of the active quasiparticles that are unique to the system at hand. The first example of a quasiparticle in the literature is the phonon: instead of focusing on the nuclei of atoms that can, in principle, be located anywhere in space, one considers their collective motion about their positions in the structure of the crystal described earlier. Scientists have studied such “soft waves” for nearly a century [2], often resorting to two popular approximations: the Born-Oppenheimer approximation, which assumes that the electrons react quickly to the displacements of the nuclei; and the harmonic approximation, which states that this response results in a restoring force equal to the displacement.
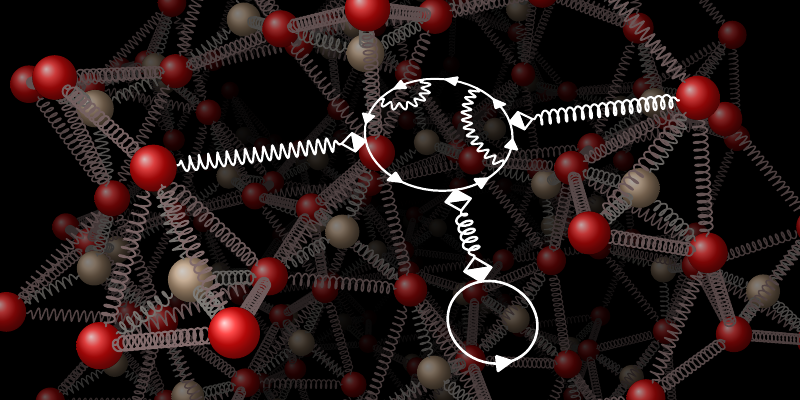
The work of Stefanucci and his colleagues builds on studies done in the middle of the last century that analyzed interactions between quasiparticles by borrowing tools from quantum field theory. In 1961, Gordon Baym published a coherent theory of electrons and phonons, where the phonon field gives the displacement of points in space and time. [3]. One of the tools mentioned above is the technique of Feynman diagrams, which represent interaction processes graphically (Fig. 1) and can be translated into mathematical formulas by simple rules. By combining such diagrams into sets of equations that are repeatedly dependent on each other, one can account for all possible processes occurring in physical reality. In 1965, Lars Hedin gave examples of this type of equations, which fully describe the electron systems interacting with each other. [4]. In a 2017 study, Feliciano Giustino combined these methods and coined the term Hedin-Baym equations in the context of state-of-the-art materials simulations – to answer many, but not all, open questions. [5].
Stefanucci and colleagues addressed several remaining issues [1]. First, they impose requirements on the electron–phonon Hamiltonian, avoiding the error of trying to solve a problem that is not well formulated from the start. They emphasize that the equilibrium state in which the theory is built is not known in advance, making it possible to establish and test the Hamiltonian iterative process. They also emphasize that this Hamiltonian cannot be written in general terms, contrary to what is often thought. Second, the team expanded on Giustino’s work [5] in systems that are driven out of alignment at any temperature – a key advance because this situation reflects experimental and technological conditions. Statistically, this general observation allows time to take difficult values. Third, the researchers thoroughly discovered the corresponding laws of Feynman diagrams and provided the first complete set of diagrammatic Hedin-Baym equations. Such equations form the basis of systematic estimation, where certain parameters are ignored, and provide a measure. [3] so that the powers that be respect the basic laws of conservation. While the effects of electrons on phonons and vice versa are best studied separately [5]here it is important that both happen at the same time.
Nowadays, parameter-free simulations of electrons and phonons rely heavily on the so-called density functional theory. [6], based on the Born-Oppenheimer and harmonic approximations. In contrast, graphic design is constant—but not constant [7]- used in conjunction with model parameterized Hamiltonians. Attempts to combine these two methods have led to the so-called reduction methods, which already exist in the electron-phonon problem. [8]. The insights gained by Stefanucci and colleagues will help to further integrate different strategies. Moreover, progressing beyond thermal equilibrium will be very important because such an extension is needed to explain the latest time-resolved spectroscopy experiments and to design better photovoltaics. Finally, given that the group’s results apply to any fermion-boson system, such as the coupled light system, many areas will benefit from this seminal work.
References
- G. Stefanucci continuous.“In and out of alignment from the beginning Theory of electrons and phonons,” Phys. Pastor X 13031026 (2023).
- F. Bloch, “On the quantum mechanics of electrons in crystal lattices,” Z. Phys. 52555 (1929).
- G. Baym, “A field-theoretic approach to solid state properties,” Ann. Phys. 141 (1961).
- L. Hedin, “A new method for calculating the single-particle Green’s function and application to the electron gas problem,” Phys. Teacher. 139A796 (1965).
- F. Giustino, “Electron-phonon interactions from first principles,” Pastor Mod. Phys. 89015003 (2017).
- S. Baroni continuous.“Phonons and related crystal properties from density-functional perturbation theory,” Pastor Mod. Phys. 73515 (2001).
- A. Marini continuous.“Body-body perturbation theory for electron-phonon interaction with density-functional theory as a starting point,” Phys. Pastor B 91224310 (2015).
- Y. Nomura and R. Arita, “From the beginning degeneracy of coupled electron-phonon systems: A constrained density-functional theory of perturbation,” Phys. Pastor B 92245108 (2015).
About the Author
Areas of Study
#Complete #Theory #Crystal #Vibrations