× nearby
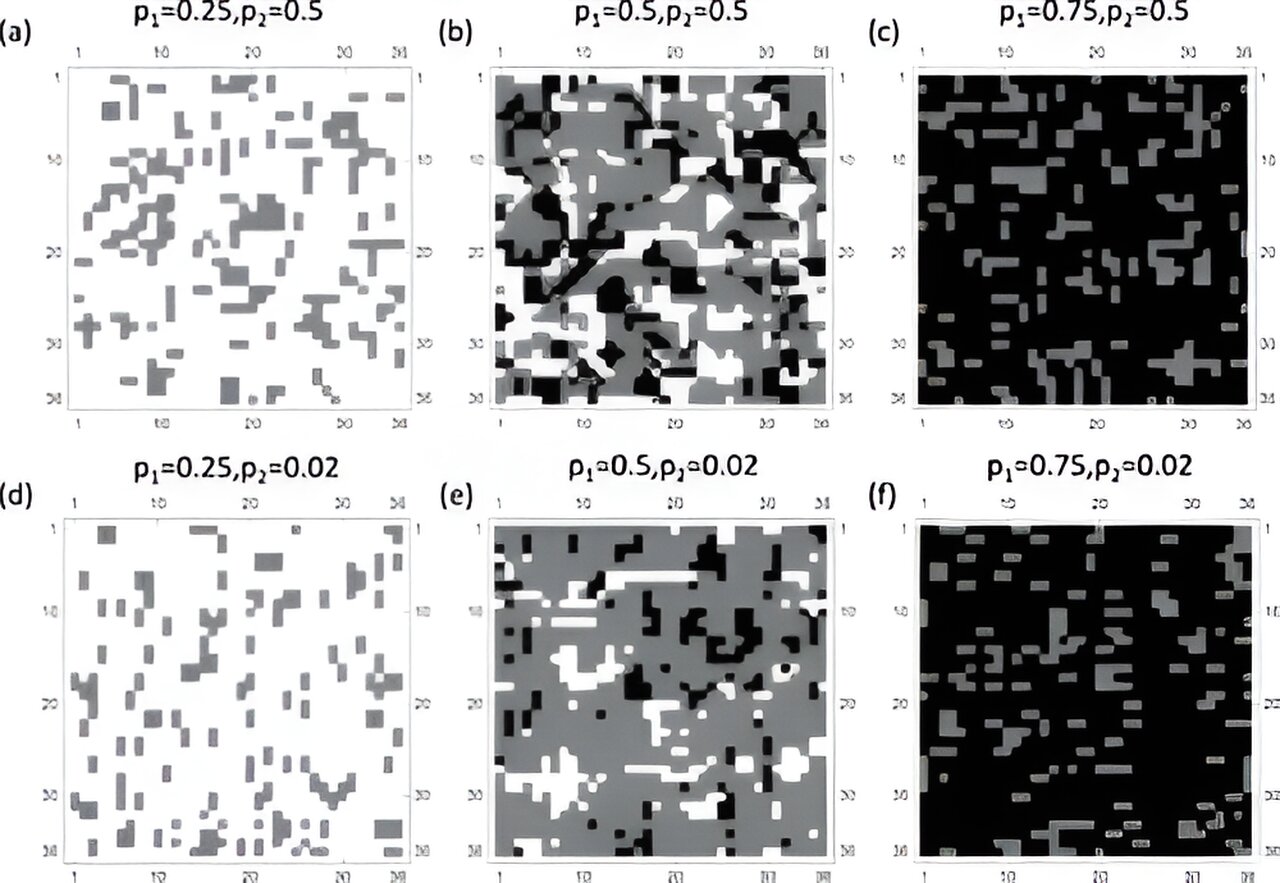
Summaries of the long-term parameters of the system size 36×36 for different values of ep1,p2. (a) p1=0.25, p2=0.5, (b) p1=0.5, p2=0.5, (c) p1=0.75, p2=0.5, (d) p1=0.25, p2=0.02, (e) p1=0.5 , p2=0.02, and (f) p1=0.75, p2=0.02. Each colored cell represents one spin. White cells do not have short Z-type stabilizers passing through them, and therefore are X-linked to each other. Dark cells do not have short-range X stabilizers that pass through them, and are associated with Z. Gray cells have many short X and Z fibers. While this color captures all long-range configurations, there may be additional short-range configurations. Credit: Physical Review B (2023). DOI: 10.1103/PhysRevB.108.024205
Window glass, at the microscopic level, exhibits an unusual mixture of structures. As a liquid, its atoms are not aligned, but as a solid, its atoms are strong, so a force applied to one atom causes them all to move.
It’s an analogy physicists use to describe a quantum state called “quantum spin-glass,” in which the quantum mechanical bits (qubits) in a quantum computer exhibit both disorder (taking seemingly ordered values) and rigidity (when one qubit turns, therefore. do all the rest). A group of Cornell researchers unexpectedly discovered the existence of this quantum level while conducting a research project designed to learn more about quantum algorithms and, relatedly, new strategies for error correction in quantum computing.
“Measuring the position of a quantum particle changes its speed and vice versa. Similarly, in qubits there is a quantity that changes when measured. We find that a certain random sequence of these incoherent measurements leads to the formation of quantum spin-glass,” said Erich Mueller, professor of physics at the College of Arts and Science (A&S). “Another implication of our work is that other types of information are automatically protected by quantum algorithms that share the characteristics of our model.”
“Subsystem Symmetry, Spin-glass Order, and Criticality from Random Measurements in a Two-dimensional Bacon-Shor Circuit” published July 31 at Physical Review B. The lead author is Vaibhav Sharma, a doctoral student in physics.
Assistant professor of physics Chao-Ming Jian (A&S) is a co-author with Mueller. All three conduct their research at the Cornell Laboratory for Atomic and Solid State Physics (LASSP).
“We’re trying to understand the general properties of quantum algorithms—things that go beyond any particular algorithm,” Sharma said. “Our strategy to uncover these universal features was to study random algorithms. We discovered that certain classes of algorithms lead to the hidden order of ‘spin-glass’. Now we are looking for other ways of hidden order and we think that this will lead us to the hidden order. A new taxonomy of quantum states.”
Random algorithms are those that include a degree of randomness as part of the algorithm – eg, random numbers to decide what to do next.
Mueller’s 2021 New Grant proposal for “Independent Quantum Error Correction” aims to simplify the construction of quantum computers by developing a new strategy for correcting quantum processor errors caused by environmental noise—that is, anything, like cosmic rays or magnetism. , that will disturb the quantum computer qubits, destroying the information.
Bits of classical computer systems are protected by error-correcting codes, Mueller said; the information is repeated so that if one bit is “turned off,” you can see it and correct the error. “For quantum computing to work now and in the future, we need to come up with ways to protect qubits in the same way.”
“The key to debugging is not to be redundant,” Mueller said. “If I send three copies of a bit, you can tell there’s a mistake by comparing the bits to each other. We borrow language from cryptography to talk about such schemes and refer to a repeated set of bits as a ‘codeword.’ ”
When they made their discovery about spin-glass order, Mueller and his team were looking at generalization, where multiple code words are used to represent the same information. For example, in the lower code, the bit “1” can be stored in 4 different ways: 111; 100; 101; and 001.
“The extra freedom one has in the quantum subsystem codes simplifies the process of detecting and correcting errors,” Mueller said.
The researchers emphasized that they were not just trying to develop an error prevention scheme when they started this research. Instead, they studied random algorithms in order to learn the general properties of all these algorithms.
“Interestingly, we found a functional structure,” Mueller said. “The most amazing thing is the existence of this spiral glass arrangement, which indicates that there is additional hidden information floating around, which must somehow be usable by the computer, although we don’t know how.”
More information:
Vaibhav Sharma et al, Subsystem symmetry, spin-glass order, and critical randomness in a two-dimensional Bacon-Shor circuit, Physical Review B (2023). DOI: 10.1103/PhysRevB.108.024205
Journal information:
Physical Review B
#promising #quantum #state #discovered #debugging #research